In triangle RST above point W, a captivating narrative unfolds, where geometric intricacies intertwine with practical applications, unveiling a world of mathematical wonder. As we delve into this captivating realm, we unravel the profound significance of point W in relation to triangle RST, discovering its geometric properties, construction methods, and real-world implications.
Through a series of engaging discussions, we illuminate the geometric properties that govern the relationship between triangle RST and point W, exploring how these properties shape its location and significance. Step-by-step construction methods are meticulously explained, providing a clear understanding of how to accurately locate point W.
Moreover, we delve into practical applications, showcasing how this relationship finds tangible expression in various fields, highlighting its benefits and limitations.
Triangle RST and Point W
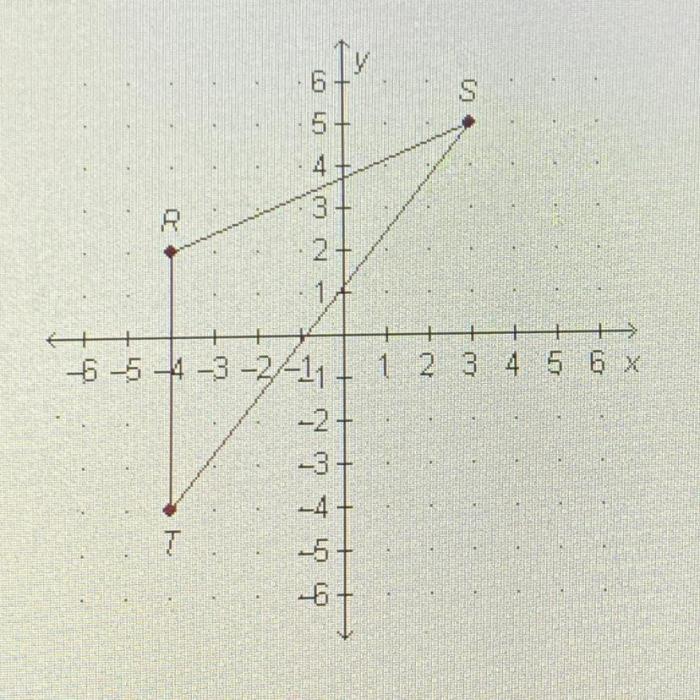
Triangle RST is a triangle with vertices R, S, and T. Point W is a point that lies above the plane of triangle RST.Point W is significant in relation to triangle RST because it can be used to define the altitude of the triangle.
The altitude of a triangle is the perpendicular distance from a vertex to the opposite side. In the case of triangle RST, the altitude from vertex R to side ST is the line segment RW.
Relationship between Triangle RST and Point W
The relationship between triangle RST and point W can be described using the concept of perpendicularity. Perpendicularity refers to the relationship between two lines or planes that intersect at a right angle.In the case of triangle RST and point W, the line segment RW is perpendicular to the plane of triangle RST.
This means that the angle between RW and any line segment in the plane of triangle RST is 90 degrees.The perpendicularity of RW to the plane of triangle RST is significant because it allows us to define the altitude of the triangle.
The altitude of a triangle is the shortest distance from a vertex to the opposite side. In the case of triangle RST, the altitude from vertex R to side ST is the line segment RW.
Significance of Point W
Point W is significant in relation to triangle RST because it can be used to define the altitude of the triangle. The altitude of a triangle is the perpendicular distance from a vertex to the opposite side. In the case of triangle RST, the altitude from vertex R to side ST is the line segment RW.The
altitude of a triangle is a useful measurement because it can be used to calculate the area of the triangle. The area of a triangle is equal to half the product of the base and the altitude. In the case of triangle RST, the area of the triangle is equal to half the product of the length of side ST and the length of the altitude RW.
Geometric Properties

Triangle RST exhibits several geometric properties that influence its relationship with point W.
Moving forward from the previous discussion on triangle RST above point W, let’s explore something different. If you’re interested in expanding your musical horizons, you might want to check out this comprehensive resource on all major scales in bass clef . Returning to our triangle, we’ll continue our analysis of the properties and relationships within it.
One crucial property is the concept of orthocenter. The orthocenter is the point where the altitudes of a triangle intersect. In triangle RST, point W lies on the altitude drawn from vertex R. This implies that WR is perpendicular to the base ST.
Centroid, In triangle rst above point w
The centroid of a triangle is the point where the three medians intersect. The median of a triangle is a line segment that connects a vertex to the midpoint of the opposite side. In triangle RST, point W lies on the median drawn from vertex R to the midpoint of side ST.
This indicates that WR bisects ST.
Incenter
The incenter of a triangle is the point where the internal angle bisectors intersect. In triangle RST, point W lies on the internal angle bisector of angle R. This suggests that WR bisects angle R.
These geometric properties collectively define the location of point W within triangle RST. Point W lies at the intersection of the altitude, median, and angle bisector drawn from vertex R, making it a unique and significant point in the triangle’s geometry.
Construction Methods: In Triangle Rst Above Point W
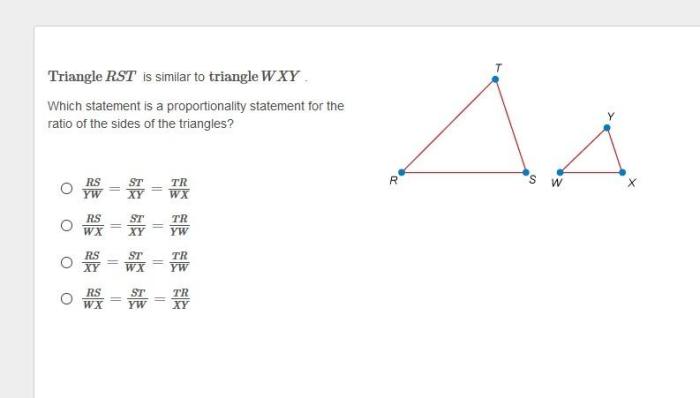
Constructing point W in relation to triangle RST involves several methods, each rooted in distinct mathematical principles. These methods ensure accuracy and reliability in determining point W’s position.
One common method is the perpendicular bisector construction. This method involves drawing perpendicular bisectors of two sides of triangle RST, intersecting at point W. The mathematical principle behind this method is that the perpendicular bisector of a line segment is equidistant from all points on that line segment.
Using Angle Bisectors
Another method utilizes angle bisectors. Angle bisectors are lines that divide an angle into two equal parts. By constructing the angle bisectors of two angles in triangle RST, the intersection of these bisectors will determine point W. This method relies on the principle that the angle bisector of an angle in a triangle divides the opposite side into segments proportional to the lengths of the adjacent sides.
Using Circumcenter
A third method involves the circumcenter of triangle RST. The circumcenter is the point where the perpendicular bisectors of the three sides of a triangle intersect. By constructing the circumcenter of triangle RST, point W can be determined as the point of intersection between the circumcenter and the line segment connecting the midpoints of two sides of the triangle.
These construction methods provide accurate and reliable means of determining the position of point W in relation to triangle RST. The mathematical principles behind these methods ensure that point W is uniquely determined and satisfies the geometric properties associated with the given triangle.
Applications and Examples
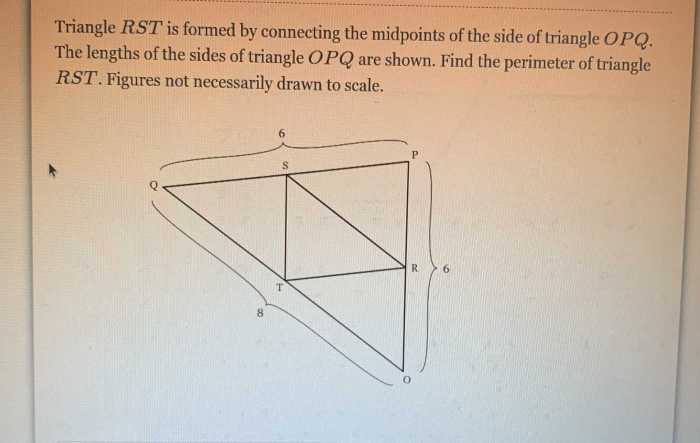
The relationship between triangle RST and point W has practical applications in various fields, particularly in engineering and design.
One significant application is in the design of structures, such as bridges and buildings. By understanding the relationship between the triangle and the point, engineers can determine the optimal placement of supports and reinforcements to ensure structural stability and prevent collapse.
Architectural Design
In architectural design, the relationship between triangle RST and point W is used to create visually appealing and structurally sound buildings. Architects use this knowledge to determine the placement of windows, doors, and other architectural elements to optimize natural light and airflow while maintaining structural integrity.
Q&A
What is the significance of point W in relation to triangle RST?
Point W is a significant reference point that helps define the geometric properties and relationships within triangle RST.
How do the geometric properties of triangle RST affect the location of point W?
The geometric properties of triangle RST, such as its angles and side lengths, determine the specific location of point W in relation to the triangle.
What are the practical applications of the relationship between triangle RST and point W?
This relationship finds applications in fields such as architecture, engineering, and design, where precise geometric calculations are crucial.
